According to an analysis by Bocconi University professor Carlo Favero, the number of people infected with the coronavirus in Lombardy, Northern Italy, is 120,000, while official figures put it at around 24,000. Hospitalizations will peak in the second week of April. With a fatality rate of 2 percent, casualties will still rise from the current 5,400 to 25,000. The alternative scenario, with no lockdown, would be much more dramatic, with a predicted cumulative toll of 160,000.
In a very interesting recent piece on ProMarket, Luigi Zingales applies a cost-benefit analysis to assess the tradeoff between minimizing the loss of human lives with lockdown measures and minimizing the restrictive impact that these measures have on the economy.
A precise assessment of this trade-off is of crucial importance. To this end, some questions on the dynamics of the virus need to be answered.
Crucial Questions Regarding the Virus’ Dynamics
What is the number of exposed and infectious subjects? What are the dynamics of hospitalization and when will it reach a peak? What is the mortality rate of the disease and how is it affected by intervention?
In this piece, I show how these questions can be answered by calibrating the baseline model of virus diffusion (the SEIR model) to the data from Lombardy, Italy.
Lombardy is an interesting case study not only because it is one of the regions in the world most dramatically affected by the disease but also because it had an institutional intervention in the form of a total lockdown, implemented on March 8th, and currently still active.
The Model-Based Answers
The simulation of the model is remarkably successful in tracking the dynamics of fatalities and hospitalized, two of the variables measured with the smaller error, over time.
The comparison of a baseline scenario in which no lockdown is implemented with an alternative scenario in which the lockdown is implemented leads to the following conclusions:
R₀ (the basic reproduction number, i.e. the number of secondary infections produced by each infected individual) is crucial: an intervention that brings R₀ from 2.3 (the average for COVID) to 0.95 brings the count of victims in Lombardy from 160,000 to 25,000 (out of a total population of 10 million).
The spreading of the disease has been discovered late in Lombardy and there is a strong underestimation of Exposed, Infected, and Removed.
As doctors from a Bergamo Hospital, heroes to the Italian people, stated: “This disaster could be averted only by a massive deployment of outreach services. Pandemic solutions are required for the entire population, not only for hospitals.”
Managing the lockdown removal carefully is crucial (historically, the second wave of viruses is the most lethal one).
How are these answers obtained?
These answers have been obtained by calibrating to data form Lombardy and simulating a standard model of virus diffusion, the SEIR (Susceptible, Exposed, Infected, Removed), which has been extensively used to track the effects of Covid-19 in China Cina.
The version considered of the SEIR model simulates dynamics for 200 days (where day 1 is determined by the appearance of patient 1). The model has been calibrated to Lombardy data by:
- Setting the initial population of Susceptible individuals to the population of Lombardy (10 million inhabitants)
- Model the intervention as a reduction in R₀, from its baseline line value from COVID data (2.3)
- The timing of the intervention has been set to match the mortality observed in the data in Lombardy on March 8, 2020, with the mortality simulated by the model. This gives day 100 as the intervention date
- Then the reduction in R₀ caused by intervention has been chosen to match the dynamics of mortality between March 8, 2020, and March 25, 2020. This gives a post-intervention R₀ of 0.95
- The hospitalization rate in the model is then chosen to match hospitalization on March 8, 2020
The Model
Model SEIR (Susceptible, Exposed, Infectious and Removed) divides total population (N) into four groups: Susceptible, those not immune to the disease; Exposed, those currently in incubation; Infectious, those infective and currently circulating; and Removed, those no longer infectious due to isolation or immunity.
The dynamics of the four groups, which determine the diffusion of the virus, are governed by a few parameters.
The dynamics of Susceptible are only dependent on the daily outflows that are determined by the probability with which a Susceptible meets and Infectious, by the basic reproduction number, R₀, and by the duration in days with which a patient is contagious.
The dynamics of Exposed have a daily inflow, which coincides with the outflow from Susceptible, and an outflow which depends on the length of the incubation period.
Likewise, the inflow to Infectious is the outflow to Exposed, and the outflow from Infectious to Removed depends on the duration with which a patient is infectious.
Removed are then grouped into three groups those who have mild symptoms and recover with no need for hospitalization, and those who need hospitalization, unfortunately, a share of those who need hospitalization does not survive.
Once values for all parameters are chosen then the model can be simulated to derived the model-based dynamics of the groups. The model can be simulated in several scenarios (typically intervention and no intervention) for policy evaluation purposes.
A user-friendly version of the model produced using R-Shiny to create an interface with the R program that simulates the underlying model is here, where the interested reader can replicate the results contained in this piece and run her own preferred parameterizations.
Parameters Choice
Here is the choice of parameters in our simulation:
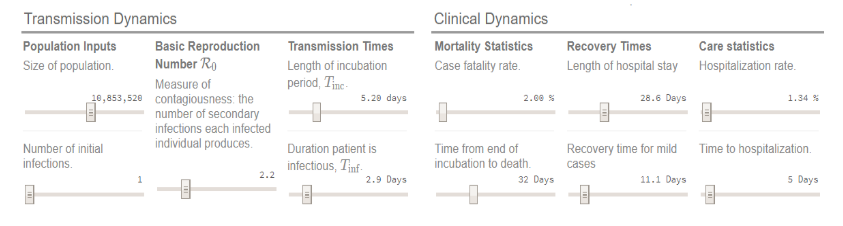
The size of the population has been chosen to match that of Lombardy. All the other parameters are calibrated to match the international evidence, with the exception of the hospitalization rate, that has been chosen to match observed hospitalization in Lombardy on the date of the implementation of the lockdown: Sunday, March 8.
Lockdown Timing and Intensity
The lockdown is introduced in a model at the date in which the model-based mortality with the baseline Basic Reproduction Number of 2.2 generates the number of victims actually observed in Lombardy on March 8th, 2020, which is 113.
The Basic Reproduction number in the alternative scenario is chosen to match mortality observed two weeks after the intervention, which is 296. This procedure delivers a post-intervention R₀ of 0.95.
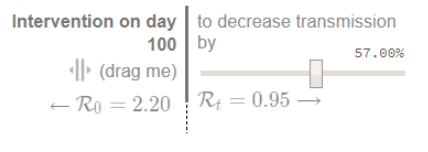
The Results
We report the simulation results by visualizing the dynamics of Exposed, Hospitalized, Fatalities, and Recovered:
EXPOSED
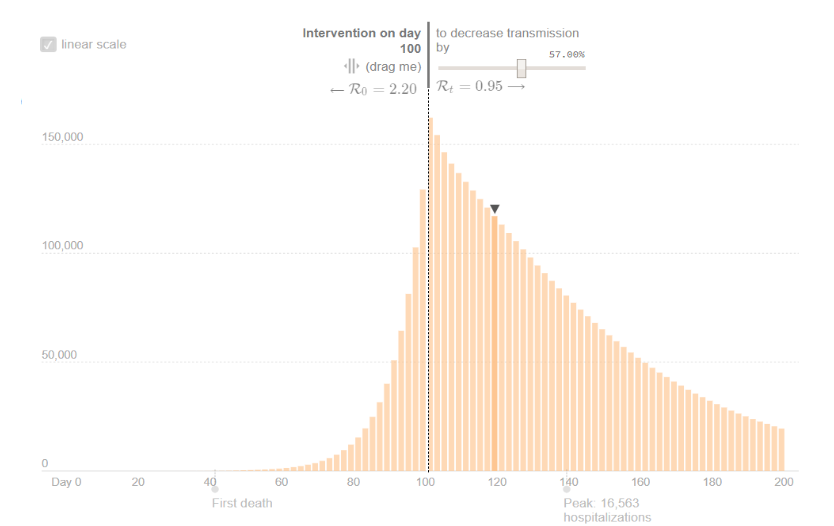
HOSPITALIZED
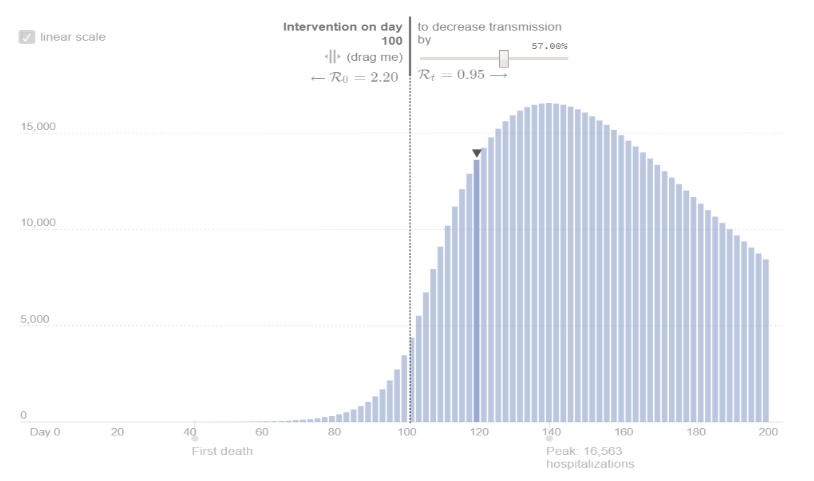
FATALITIES
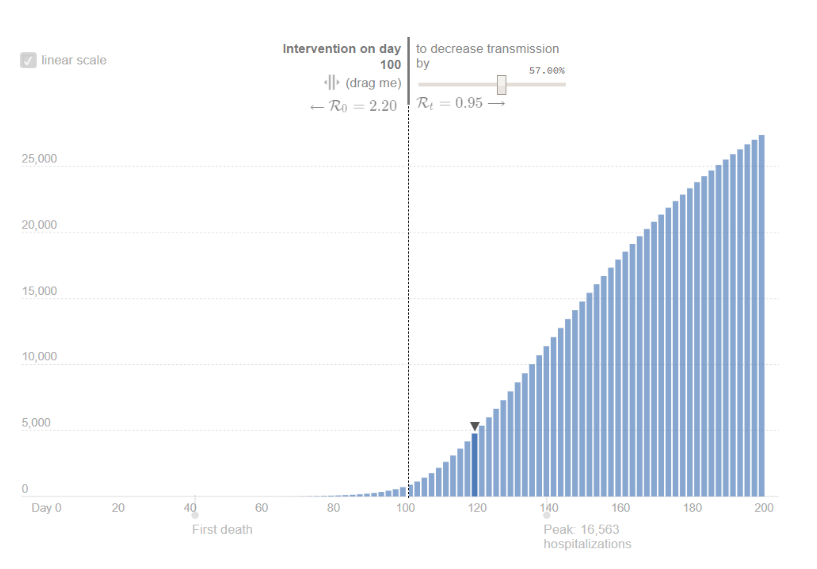
RECOVERED
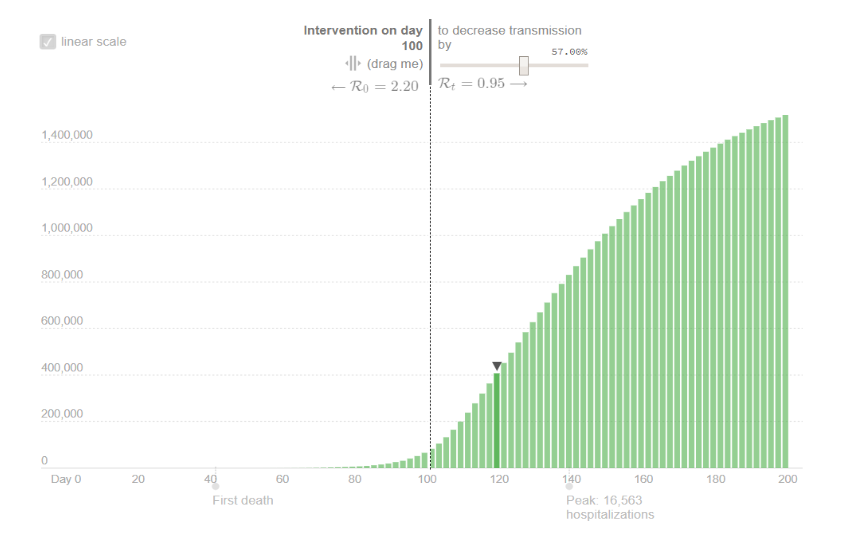
The main result of the simulation can be summarized as follows:
The Exposed are close to 120,000—a number much higher than the official figures, which stand at around 24,000. This number has reached a peak with the lockdown and is decreasing from then onwards
The dynamic of Hospitalization predicts a peak at around 15,000 cases, which will be reached 40 days after the intervention, in the second week of April 2020.
Fatalities, with a fatality rate of 2 percent, reach a cumulative value of 25,000 individuals with the intervention. The alternative scenario is much more dramatic, with a predicted cumulative value of 160,000.
Please note that a 2 percent mortality rate, which is in line with the international data, predicts the dynamics of the data very well. A 2 percent rate is very different from the official figures, but those figures are obtained by dividing fatalities by the measured number of Exposed people in Lombardy, a figure that is grossly underestimating the model-based Exposed.
The simulation also has some positive news: the number of recovered people reaches400,000 two weeks after the intervention.
However, it is clear that the most crucial parameter is R₀: bringing it below 1 means a great achievement in saving lives. This clearly speaks for the importance of citizens abiding by the rules of the current lockdown, but it should also urge policymakers to devise exit strategies from the lockdown that will prevent the basic reproduction number to jump back to the initial pre-intervention level.
Toward this end, ideas like the widespread testing and targeted isolation supported by Paul Romer in a recent piece on ProMarket and the proposal made on VoxEU by Andrea Ichino et al., which involves gradually sending the young who face the lowest risks back to work on a voluntary basis, should be seriously considered.
ProMarket is dedicated to discussing how competition tends to be subverted by special interests. The posts represent the opinions of their writers, not necessarily those of the University of Chicago, the Booth School of Business, or its faculty. For more information, please visit ProMarket Blog Policy.